POJ2663 | 哈喽哈咯

Written by razrlele 20:37 March 27, 2015

Tri Tiling

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 8737		Accepted: 4554

Description

In how many ways can you tile a 3xn rectangle with 2×1 dominoes?
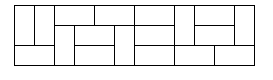
Here is a sample tiling of a 3×12 rectangle.

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

-1

Sample Output

153

2131

Source

Waterloo local 2005.09.24

简单DP题目。

题意是给定一个3×n的矩形，然后用2×1的矩形来填满，问有多少种不同的填充方案。

令3×2为一个单位，首先要明白的是如果n为奇数的话无论如何也填不满。

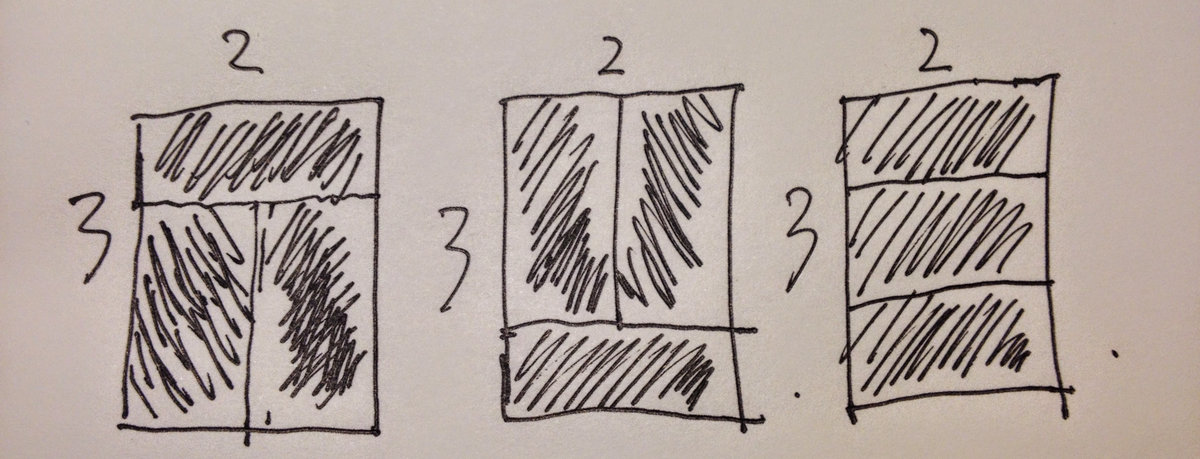
对于每一个单位矩形，有下列三种方式可以填满：

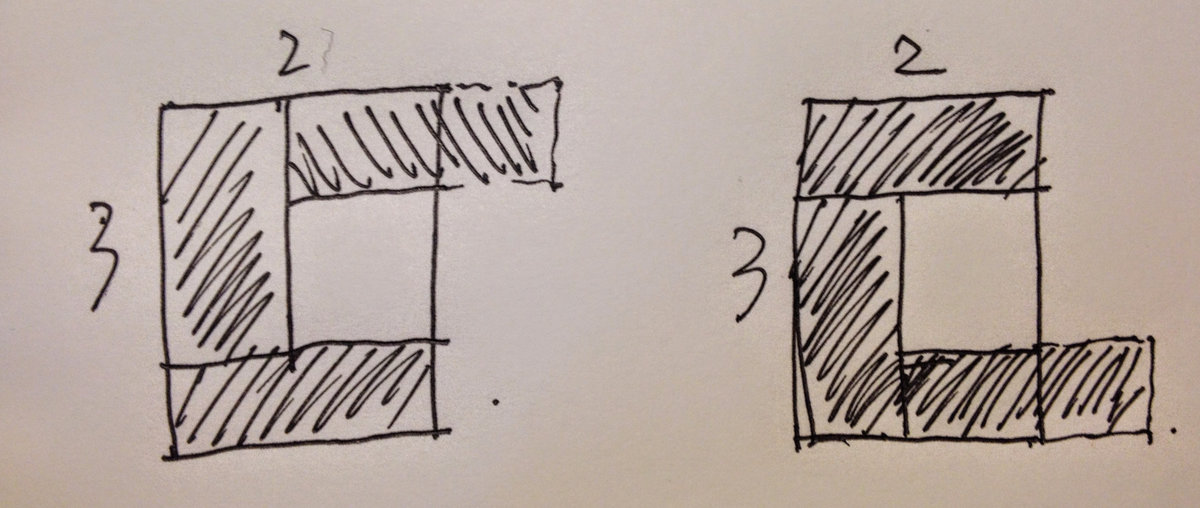
然后也有下列两种方式可以作为衔接：

进而可以推出 DP[i] = 3×DP[i-1] + 2×(DP[i-2]+DP[i-3]+Dp[i-4]+ … + DP[0])

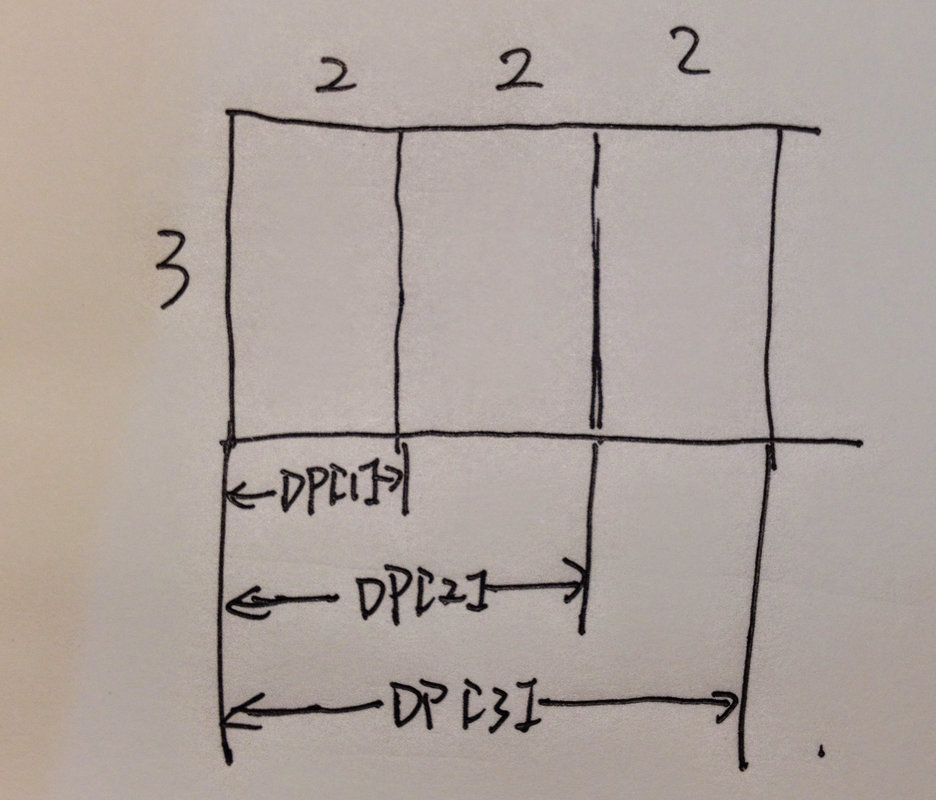
想要理解清楚这个DP思想，可以先看看下图对于DP[i]的定义：

如图所示DP[i]和DP[i-1]是前者包含后者的关系，刚开始的时候总是喜欢理解成互相独立的关系所以很容易昏了头。

DP算法其实就是数学归纳法，关键在于找出那个状态转移方程。

再来看这道题目，因为数据范围只有30，所以直接打表即可。

/********************************************************

* File Name: poj2663.cpp

* Author: razrLeLe

* Mail: razrlele@gmail.com

* Homepage: https://yueyu.io

* Created Time: Fri 27 Mar 2015 12:12:30 AM CST

******************************************************/

#include "vector"

#include "set"

#include "deque"

#include "queue"

#include "algorithm"

#include "functional"

#include "iostream"

#include "cstdio"

#include "cmath"

#include "cstdlib"

#include "string"

#include "cstring"

#include "string.h"

#include "map"

#include "cctype"

#include "list"

#include "stack"

using namespace std;

#define INF 0x3f3f3f3f

#define LOCAL

int main()

{

#ifdef LOCAL

freopen("/home/razrlele/build/data.txt", "r", stdin);

freopen("/home/razrlele/build/out.txt", "w", stdout);

#endif

int dp[16];

dp[0] = 1;

int n;

for(int i = 1; i < 16; i++)

{

dp[i] = 3*dp[i-1];

for(int j = 0; j <= i-2; j++)

dp[i] += 2*dp[j];

}

while(cin >> n && n != -1)

{

if(n%2)

cout << 0 << endl;

else

cout << dp[n/2] << endl;

}

return 0;

}