UVAOJ10012 | 哈喽哈咯

Written by razrlele 19:58 March 6, 2015

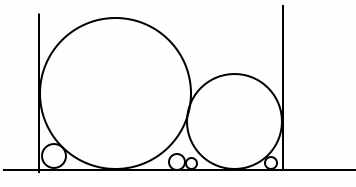
题意其实就是是把一堆圆球放在一个箱子里，因为箱子的最小高度是固定的（即最大的圆的直径），所以题目要求最小的箱子宽是多少，注意球必须同时接触地面，即不能层叠起来，这里一开始很自然地想到了直接全排列暴力（因为球最多只有8个），但是下图的这种情况很容易被忽略，这也是这个题目的AC率如此之低的原因：

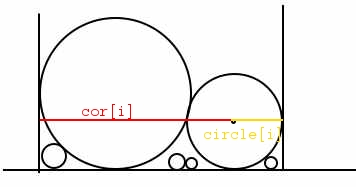
首先假设每一个球都在靠在最左边，然后求除左边第一个球之外的所有球相对于最左边最大距离，保存在一个数组cor[10]，然后求cor[i]+circle[i]最大值即为最小的箱子宽度。

/********************************************************

* File Name: uvaoj10012.cpp

* Author: razrLeLe

* Mail: razrlele@gmail.com

* Homepage: https://yueyu.io

* Created Time: Thu 05 Mar 2015 05:57:55 PM CST

******************************************************/

#include "vector"

#include "set"

#include "deque"

#include "queue"

#include "algorithm"

#include "functional"

#include "iostream"

#include "cstdio"

#include "cmath"

#include "cstdlib"

#include "string"

#include "cstring"

#include "string.h"

#include "map"

#include "cctype"

#include "list"

#include "stack"

using namespace std;

#define INF 0x3f3f3f3f

#define LOCAL

int m;

double circle[10];

double ans;

double dis(double a, double b){

double x = max(a, b), y = min(a, b);

return sqrt((x+y)*(x+y)-(x-y)*(x-y));

}

void cal()

{

double cor[10];

cor[0] = circle[0];

for(int i = 1; i < m; i++){

cor[i] = circle[i];

for(int j = 0; j < i; j++){

double tmp = dis(circle[i], circle[j])+cor[j];

cor[i] = max(tmp, cor[i]);

}

double tmpsum = -1;

for(int i = 0; i < m; i++)

tmpsum = max(cor[i]+circle[i], tmpsum);

ans = min(tmpsum, ans);

return ;

}

void solve()

{

do{

cal();

}while(next_permutation(circle, circle+m));

return ;

}

int main()

{

#ifdef LOCAL

freopen("/home/razrlele/build/data.txt", "r", stdin);

freopen("/home/razrlele/build/out.txt", "w", stdout);

#endif

int numcase;

scanf("%d", &numcase);

while(numcase--)

{

scanf("%d", &m);

for(int i = 0; i < m; i++ ){

scanf("%lf", &circle[i]);

}

sort(circle, circle+m);

ans = INF;

solve();

printf("%.3lf\n", ans);

}

return 0;

}