Word2Vec算法是NLP领域一个里程碑式的工作,它可以通过训练把文本内容映射到一个K维的向量,这样就很方便继续在其他一些算法领域里面使用,比如推荐系统或者广告点击率预估等等。它是在2013年由当时还在Google工作的Tomas Mikolov发表,主要两篇论文是《Distributed Representations of Words and Phrases and their Compositionality》和《Efficient Estimation of Word Representations in Vector Space》.
N-gram
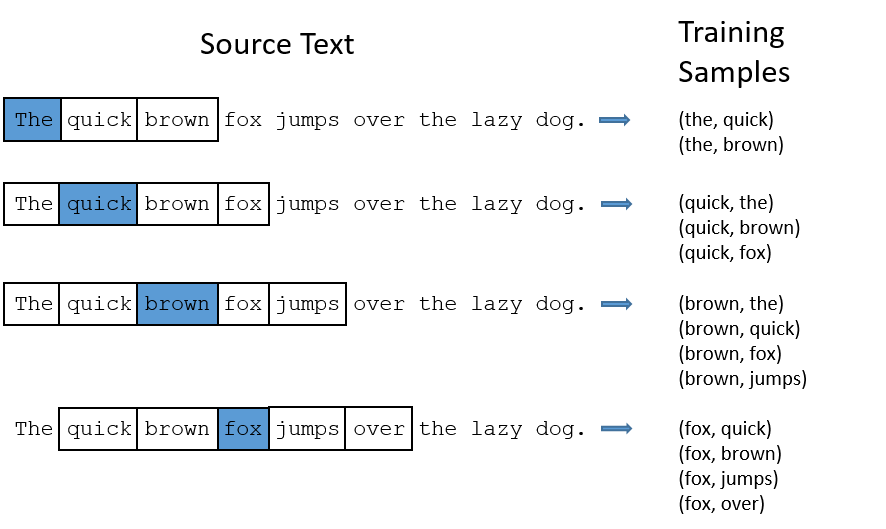
Word2vec主要是通过词的上下文来学习词的表征含义,所以在预处理训练数据的时候,采用了n-gram语言模型,即将一个词前后2n个词作为训练数据,如下图所示就是n=2时的情形:
其实n-gram本身就可以用来构建一个词与词之间的矩阵,用来表示每一个词与上下文之间的关系,比如下图就是一个n=1时候的n-gram词矩阵:

但是当词很多的时候,虽然也可以用到矩阵分解等方法,但是计算的时空复杂度还是比较大,应用不是很方便。
CBOW
Continuous Bag of Words Model 简称CBOW,是Word2Vec的网络模型的一种,其网络结构主要如下图:
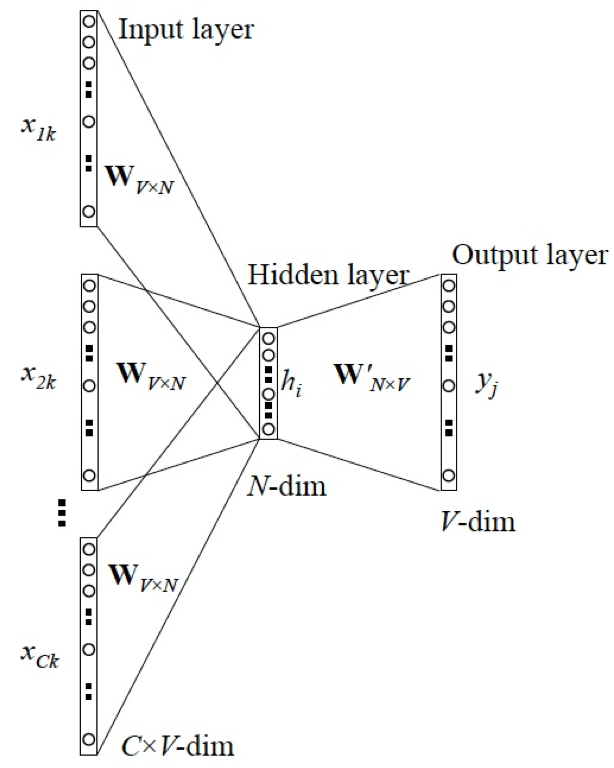
左边是选定词的上下文,即n-gram中前后m个词,中间是隐藏层,最右边就是中间词,V是词表大小,N是选定的向量维度,简单来看就是用上下文来预测词本身。具体算法如下,其中窗口大小为m,向量维度为n,词的总个数为\(\vert V \vert\):
- 用one-hot编码生成2m个向量:
\((x^{(c-m)}, … , x^{(c-1)}, x^{(c+1)}, … , x^{(c+m)})\) - 基于步骤1初始化生成的2m个向量,乘上输入矩阵\(\mathcal{V} \in \mathcal{R^{n \times \vert V \vert}}\):
\( ( \mathcal{v}_{(c-m)}=\mathcal{V}x^{(c-m)}, \mathcal{v}_{(c-m+1)}=\mathcal{V}x^{(c-m+1)}, …, \mathcal{v}_{(c+m)}=\mathcal{V}x^{(c+m)} )\) - 对所有的向量取平均,得到:
\(\hat{\mathcal{v}}=\frac{\mathcal{v}_{c-m}+\mathcal{v}_{c-m+1}+ … + \mathcal{v}_{c-m} }{2m}\) - 然后乘上一个输出层矩阵\(\mathcal{U} \in \mathcal{R^{n \times \vert V \vert}}\)得到:
\( z = \mathcal{U}\hat{\mathcal{v}}\) - 对结果取一个softmax:
\(\hat{y} = softmax(z) \) - 重复迭代使得\(\hat{y}\)接近真实值\(y\),就是中间词的one-hot编码。
确定了迭代过程过后就要确定loss,在Word2Vec里面使用的是交叉熵作为loss,即\(\mathcal{H}(\hat{y}, y)=-y_{i}log y_{i}\),接下来就可以确定优化目标为:
\(\begin{aligned} minimize \mathcal{J} &= -logP(w_{c}|w_{c-m}, …, w_{c-1}, w_{c+1}, …, w_{c+m} \\ &= -logP(u_{c}|\hat{v}) \\ &= -log\frac{ exp(u_{c}^{T} \hat{v}) }{ \sum^{\vert V \vert }_{j=1} exp(u_{j}^{T}\hat{v}) } \\ &= -u^{T}_c\hat{v}+log\sum^{\vert V \vert}_{j=1} exp(u_{j}^{T}\hat{v}) \end{aligned}\)
然后就可以开始用梯度下降来优化计算了。
Skip-gram
Skip-gram则是与CBOW完全相反的一种模型,CBOW用周围词来预测中间词,Skip-gram则是用中间词来预测周围词,其网络模型如下图所示:
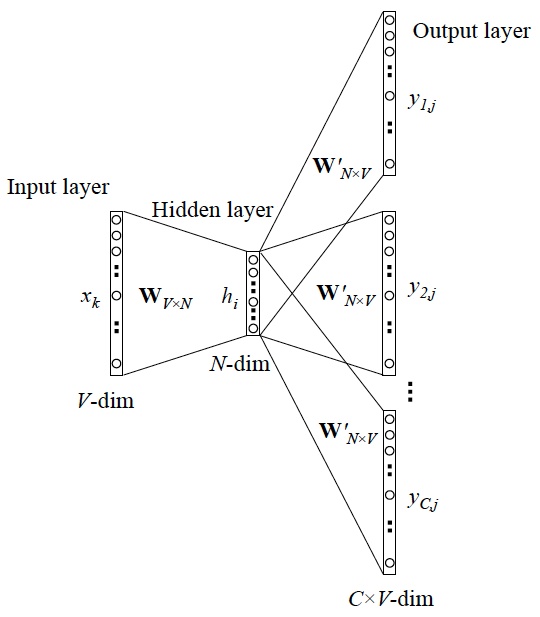
其训练过程也与CBOW相似:
- 生成一个one-hot编码的向量\(x\)
- 乘上输入矩阵\(\mathcal{V} \in \mathcal{R^{n \times \vert V \vert}}\)得到:
\(v_{c} = \mathcal{V}x\) - 因为这里只有一个向量,所以直接令\(\hat{v} = v_{c} \)
- 利用输出层矩阵\(\mathcal{U} \in \mathcal{R^{n \times \vert V \vert}}\), \(u=\mathcal{U}\mathcal{v}_{c}\),得到2m个向量:
\(u_{c-m}, …, u_{c-1}, u_{c+1}, …, u_{c+m}\) - 对每一个向量取softmax,\(y=softmax(u)\)
- 不断迭代使得所求值逼近真实的\(y^{(c-m)}, …, y^{(c-1)}, y^{(c+1)}, …, y^{(c+m)} \)
如同CBOW的目标函数,也使用交叉熵作为loss,稍有不同的是使用了朴素贝叶斯来拆概率计算:
\(\begin{aligned} minimize J &= -logP(w_{c-m}, …, w_{c-1}, w_{c+1}, …, w_{c+m}) \\ &= -log\prod^{2m}_{j=0, j \neq m} P(w_{c-m+j}|w_{c}) \\ &= -log\prod^{2m}_{j=0, j \neq m} P(u_{c-m+j}|v_{c}) \\ &= -log\prod^{2m}_{j=0, j \neq m} \frac{exp(u^{T}_{c-m+j}v_{c})}{\sum^{\vert V \vert}_{k=1}exp(u_{k}^{T}v_{c})} \\ &= -\sum^{2m}_{j=0, j \neq m} u^{T}_{c-m+j}v_{c} + 2m log\sum^{\vert V \vert }_{k=1} exp(u^{T}_{k}v_{c}) \end{aligned}\)
根据作者的建议,Skip-gram一般速度更慢一点,但是对低频词效果更好,而CBOW则训练速度更快一点。
Hierarchical Softmax 和Negative Sampling
在计算的时候,作者还使用了两个Trick来优化训练速度,第一个是hierarchical softmax,即首先根据词频对词表构建Huffman编码,这样在计算目标函数的时候,\(\sum_{j=1}^{\vert V \vert}\)就变成了\(\sum_{j=1}^{log \vert V \vert}\)了,计算效率大大提高,Word2Vec中,采用了二元逻辑回归的方法,即规定沿着左子树走,那么就是负类(Huffman树编码1),沿着右子树走,那么就是正类(Huffman树编码0),一开始我纠结了半天的Huffman中的非叶子节点意义是什么,但是关键在于Huffman树有用的只是叶子节点,那些非叶子节点可以看成一个隐变量,不需要管实际意义是什么,词频越高的词层数越高,也更容易被学到,这个也符合我们的需求。
第二个则是Negative Sampling,在更新输出层矩阵的时候,只去更新positive word和一部分negative word单词,这个一部分negative word是通过unigram distribution来选择的,出现频次越高的单词更容易被选作negative words,从而可以降低计算量。
Sub-sampling
除了hierarchical softmax和negative sampling,Word2Vec也用到了NLP中常用的sub-sampling来加速训练,选定概率\(P=1-\sqrt{\frac{sample}{freq(w)}}\)来随机删掉一些词,类似于”the”, “a”等等,这些词一般出现频率比较高但是意义不大。
References
- Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Distributed Representations of Words and Phrases and their Compositionality. In Advances in Neural Information Processing Systems.
- Mikolov, T., Corrado, G., Chen, K., & Dean, J. (2013). Efficient Estimation of Word Representations in Vector Space. Proceedings of the International Conference on Learning Representations (ICLR 2013).
- 邓澍军、陆光明、夏龙,《Deep Learning 实战之 word2vec》
- http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model
- https://cs224d.stanford.edu/lecture_notes/notes1.pdf
- https://www.cnblogs.com/pinard/p/7243513.html
- https://www.cnblogs.com/pinard/p/7249903.html