Logistic Regression | 哈喽哈咯

Written by razrlele 21:21 October 6, 2018

逻辑斯谛回归因为其易于实现，可解释性强，已经成为了工业界应用最广泛的机器学习算法。这篇文章主要讨论的是二项逻辑斯谛回归 (binominal logistic regression)，以下简称LR。

定义

首先引入一个sigmoid函数，其数学形式为：

\(g(x)=\frac{1}{1+e^{-x}}\)

函数图像是：

从函数图像可以看出来是一个s形的曲线，在远离0的地方会很快接近0或者1，至于为什么用的是这个函数，Rudan Chen在其博客中有讲到Logistic Regression的起源[1]，其实也只是统计学家们根据人类社会中的一些统计数据拍出来的，最后形式简单效果好。而sigmoid函数就是LR的决策函数。

对于二项逻辑斯谛回归，是如下的条件概率分布：

\(P(Y=1|x)=\frac{e^{-(w \times x+b)}}{1+e^{-(w \times x+b)}} \\ P(Y=0|x)=\frac{1}{1+e^{-(w \times x+b)}}\)

这里\(x \in R^n\)是输入，\(Y \in \{0, 1\} \)是输出，\(w \in R^n\) 和 \( b \in R\) 是参数，\(w\)是权值向量，\(b\)是偏置(bias)， \(w \times x\)是\(w\)和\(x\)的内积。

为了方便起见，可以把\(w\)看成比\(x\)多一维的向量，而\(b\)就是多出的那一维度的值。在实现的时候则可以在读取训练数据\(x\)的时候，多添加一维，并赋值为1，然后再去把\(w\)初始化为于\(x\)一样维度的向量，这样就不用在代码里面多加一个\(b\)了。

损失函数

设LR模型为：

\(P(Y=1|x)=\pi(x), P(Y=0|x)=1-\pi(x)\)

其中\(\pi(x)=g(w \times x+b)\)

则似然函数为：

\(\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{(1-y_i)}\)

对似然函数取对数：

\(L(w)=\sum_{i=1}^N[{y_i}log\pi(x_i)+(1-y_i)log(1-\pi(x_i))]\)

然后令：

\(J(w)=\frac{-1}{N} \times L(w)\)

这里的\(J(w)\)就是整个数据集的平均log损失，可以发现\(J(w)\)也是整个数据集的平均熵，所以从另一个角度来说，平均熵越小就越拟合数据集，接下来求解令\(J(w)\)取得极小值的\(w\)其实也是求解令整个的数据集的平均熵极小的\(w\)。

求解

这里用先用梯度下降来求解\(w\)，从而使得\(J(w)\)取得极小值。梯度下降(Gradient Descent)又叫作最速梯度下降，是一种迭代求解的方法，通过在每一步选取使目标函数变化最快的一个方向调整参数的值来逼近最优值。

对于梯度下降的算法描述如下：

选择梯度方向，即\( J'(w_i)\)
选择步长，更新参数，\(w_{i+1}=w_i-\alpha_i J'(w_i)\)
重复1，2直至满足条件

所以接下来就要求出\( J'(w)\).

这里先来看\( g'(x)\):

\(\begin{aligned} g'(x) &= \frac{\partial g(x)}{\partial x} \\ &= \frac{e^{-x}}{(1+e^{-x})^2} \\ &=\frac{1}{1+e^{-x}} \frac{e^{-x}}{1+e^{-x}} \\ &= g(x)(1-g(x))\end{aligned}\)

所以对于\( J'(w)\)

\(\begin{aligned} J'(w) &= \frac{-1}{N} \sum_{i=1}^N[\frac{{y_i}{x_i}{g'(w{x_i})}}{g(w{x_i})}+\frac{(1-y_i)(-x_i){g'(w{x_i})}}{1-g(w{x_i})}] \\ &= \frac{-1}{N} \sum_{i=1}^N[{y_i}{x_i}(1-g(w{x_i})) – {x_i}(1-y_i)g(w{x_i})] \\ &= \frac{-1}{N} \sum_{i=1}^N{x_i} ({y_i} -g(w{x_i}))\end{aligned}\)

然后为了防止过拟合，要加一个正则项:

\(J(w)=\frac{-1}{N} \times L(w) + \lambda \Phi(w)\)

\(\lambda\) 是用来控制正则项惩罚力度的，取L1正则项的时候\(\Phi(w)=\|w\|\), 取L2正则项的时候 \(\Phi(w)= \sum_{i=1}^N w_i^2\), L1正则化会导致参数值变为0，但是L2却只会使得参数值减小，所以L1更容易产生稀疏解，适合做特征筛选，在一定程度上也适合做防止过拟合，L2则比较适合作防止过拟合。

实现

采用的数据集是台大的libsvm格式样例数据[3].

首先需要注意的是预测值是有可能为0或者1的，这样在计算loss的时候可能会报错，可以使用numpy.clip来处理预测值，保证数据在eps到1-eps之间。跑了十万次迭代过后准确率基本上跟的sklearn版本差不多，就是速度慢了一点，毕竟只是一个的很基础的实现，还有很多优化空间。

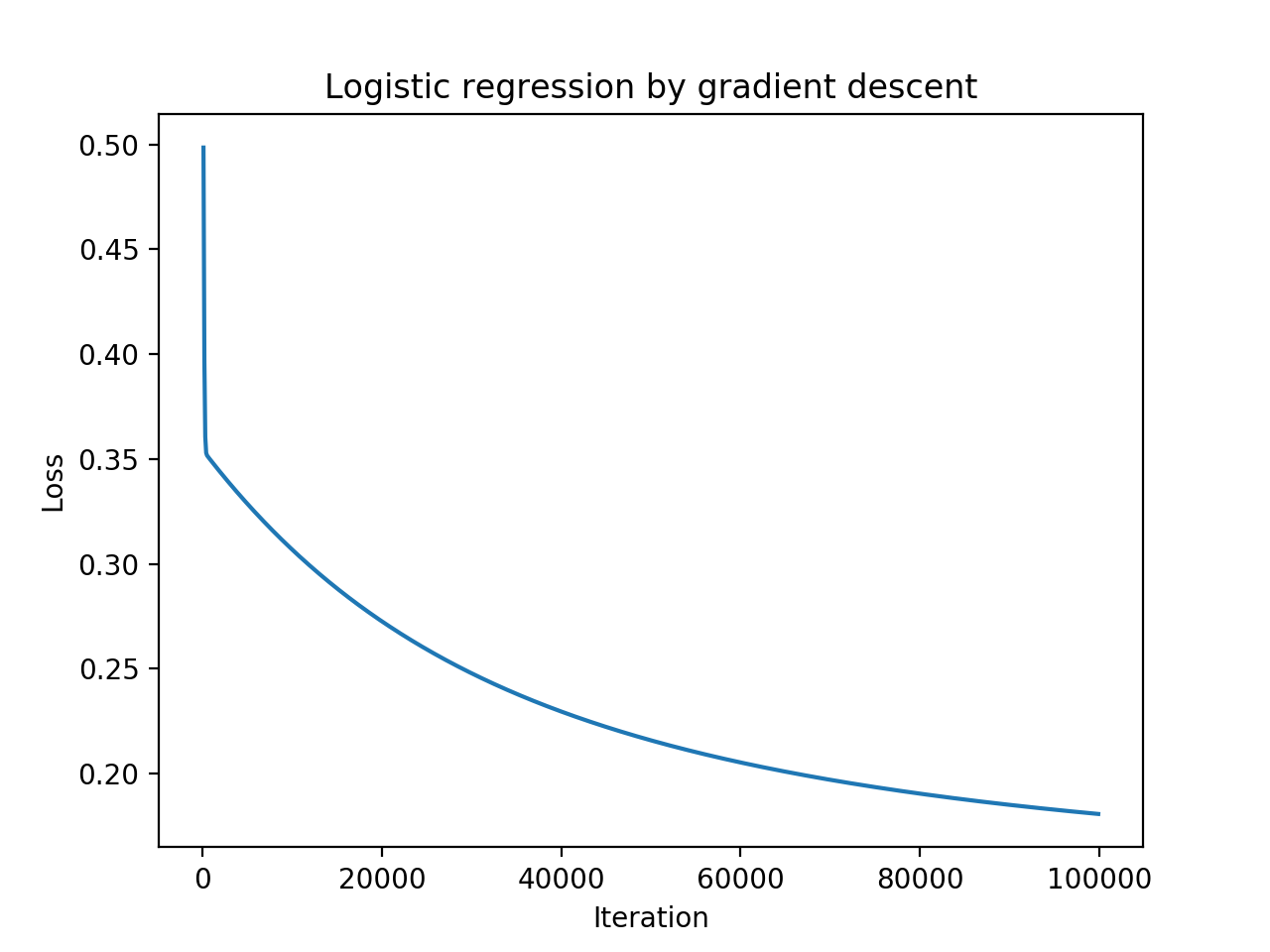
以下就是Python版本的LR Gradient Descent 实现：

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

#!/usr/bin/env python3

# -*- coding: utf-8 -*-

'''

Author: razrlele

Email: razrlele@gmail.com

Description: Logistic regression by gradient descent

'''

import numpy as np

import math

from sklearn.datasets import load_svmlight_file

from scipy.sparse import csr_matrix, hstack

import argparse

import pylab as pl

def sigmoid(z):

gz = 1.0/(1.0+math.exp(-1.0*z))

return gz

def log_loss(y, y_pred, w, eps=1e-15, lam=0.01 ):

y_pred = np.clip(y_pred, eps, 1-eps) # to avoid 0 or 1 in y_pred

return np.sum( y*np.log(y_pred) + (1-y)*np.log(1-y_pred) ) + (1/2.0)*lam*np.sum(w*w.T)

def cost_function(X, y, w, lam=0.01):

m = len(y)

y_pred = (X*w.T).toarray().flatten()

y_pred = list(map(sigmoid, y_pred))

J = (-1/float(m)) * log_loss(y, y_pred, w) + (1/(2.0*m)) * lam * np.sum(w*w.T)

return J

def error_function(X, y, w, thres=0.5):

y_pred = (X*w.T).toarray().flatten()

y_pred = list(map(sigmoid, y_pred))

n = len(y_pred)

return sum(1 for i in range(n) if int(y_pred[i] > thres) != y[i]) / float(n)

def w_derivative(X, y, w):

m = float(len(y))

y_pred = (X*w.T).toarray().flatten()

y_pred = list(map(sigmoid, y_pred))

delta_w = (-1/m) * (X.T*(y-y_pred)).T

return delta_w

def gradient_desent(X, y, w, alpha=0.001, lam=0.01):

m = len(y)

delta_w = w_derivative(X, y, w)

new_w = w - alpha*(csr_matrix(delta_w)) - lam*w/float(m)

return new_w

def logistic_regression(X, y, X_t, y_t, num_iters=100000):

w = csr_matrix(np.random.random((1, X.shape[1]))) # w_0, w_1, ... , w_n

res = open("./res.txt", "w")

iters = []

cost = []

for i in range(num_iters):

w = gradient_desent(X, y, w)

if i %100 == 0 and i > 0:

J = cost_function(X, y, w)

E_test = error_function(X_t, y_t, w)

E_train = error_function(X, y, w)

iters.append(i)

cost.append(J)

res.write(str(i)+"\t"+str(J)+"\n")

print("Cost is ", J)

print("Error in test is ", E_test)

print("Error in train is ", E_train)

res.close()

def sklearn_test(X, y, X_t, y_t):

from sklearn.linear_model import LogisticRegression

clf = LogisticRegression()

clf.fit(X, y)

print("sklearn score", clf.score(X_t, y_t))

def plot_res():

iters = []

cost = []

count = 1

with open("./res.txt", "r") as fin:

for line in fin:

i, j = line.strip().split("\t")

iters.append(float(i))

count+=1

cost.append(float(j))

pl.xlabel('Iteration')

pl.ylabel('Loss')

pl.title('Logistic regression by gradient descent')

pl.plot(iters, cost)

pl.show()

def load_data(fname):

X, y = load_svmlight_file(fname)

X = csr_matrix( hstack((np.ones([X.shape[0], 1]), X)) )

return X, y

def parse_arg():

arg_parser = argparse.ArgumentParser(description='data_preprocess')

arg_parser.add_argument('--plot', type=bool, default=False, help='Plotting the result')

arg_parser.add_argument('--lrgd', type=bool, default=False, help='Run logistic regression by gradient descent')

arg_parser.add_argument('--sklearn', type=bool, default=False, help='Run LR train by sklearn')

args = arg_parser.parse_args()

return args

def main():

args = parse_arg()

X, y = load_data("./train.1")

X_t, y_t = load_data("./test.1")

if args.plot:

plot_res()

elif args.lrgd:

logistic_regression(X, y, X_t, y_t)

elif args.sklearn:

sklearn_test(X, y, X_t, y_t)

pass

if __name__ == "__main__":

main()

参考

[1]【机器学习算法系列之二】浅析Logistic Regression

[2]Logistic Regression 模型简介

[3]Index of /~cjlin/papers/guide/data

[4] 李航，《统计学习方法》

[5] 周志华，《机器学习》