| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 9644 | Accepted: 3131 |
Description
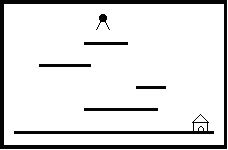
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。
Input
第一行是测试数据的组数t(0 <= t <= 20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000,-20000 <= X, X1[i], X2[i] <= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
Output
Sample Input
|
1 2 3 4 5 |
1 3 8 17 20 0 10 8 0 10 13 4 14 3 |
Sample Output
|
1 |
23 |
Source
思路
Jimmy每落到一个平台上面,要么走到左边跳下去,要么走到右边跳下去,所以这个题目就可以看作求每一个平台左右两端到达地面的最短时间,其中出发点视作第0个宽度为0高度为Y的平台,然后把所有的跳板由高到低按照1到N进行排序,就可以得出第i个平台分别和其左边缘和右边缘正下方的平台downl, downr满足关系:
|
1 2 3 |
rightMinTime[i] = plant[i].h - plant[downr].h + min( leftMintime[downr]+ plant[i].r - plant[downr].l, rightMinTime[downr] + plant[downr].r - plant[i].r); leftMinTime[i] = plant[i].h - plant[downl].h + min( leftMintime[downl]+ plant[i].l - plant[downl].l, rightMinTime[downl] + plant[downl].r - plant[i].l); |
如果左边或者右边正下方没有平台的话,则考虑当前平台自身的高度是否大于MAX,如果是的话就此路不同,否则直接返回当前平台的高度。
这样的话就找到了DP的状态转移方程。
然后就是递归的时候要注意存储当前求出的平台左右最短时间,否则的话会有冗余计算从而TLE。
在评论区里面看到了一个trick:
不过我似乎没有对这个做特别处理,最后也是AC了。。。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 |
/* * File Name: poj1661.cpp * Author: razrLeLe * Mail: razrlele@gmail.com */ #include <vector> #include <set> #include <deque> #include <queue> #include <algorithm> #include <functional> #include <iostream> #include <cstdio> #include <cmath> #include <cstdlib> #include <string> #include <cstring> #include <string.h> #include <map> #include <cctype> #include <list> #include <stack> #define forn(i, m, n) for (int i = int(m); i < int(n); i++) typedef long long ll; using namespace std; #define INF 0x3f3f3f3f #define LOCAL const int maxn = 1007; struct board { int l, r, h; } P[maxn]; int leftMinTime[maxn], rightMinTime[maxn]; //int P[maxn][3]; //[i][0] left x1 [i][1] right x2 [i][2] h int N, X, Y, MAX; bool cmp(board a1, board a2) { return a1.h > a2.h; } int findLeft(int k); int findRight(int k); int main(int argc, char** argv) { #ifdef LOCAL freopen("/home/razrlele/build/data.txt", "r", stdin); freopen("/home/razrlele/build/out.txt", "w", stdout); #endif int T; cin >> T; while (T--) { cin >> N >> X >> Y >> MAX; P[0].l = P[0].r = X; P[0].h = Y; leftMinTime[0] = rightMinTime[0] = -1; forn(i, 1, N + 1) { leftMinTime[i] = rightMinTime[i] = -1; cin >> P[i].l >> P[i].r >> P[i].h; } sort(P, P + N + 1, cmp); cout << findRight(0) << endl; } return 0; } int findRight(int k) { int down = -1; forn(i, k + 1, N + 1) if ((P[k].r - P[i].r) * (P[k].r - P[i].l) <= 0) { down = i; break; // if( P[k].h - P[i].h > MAX) // return INF; // return P[k].h - P[i].h + min( findLeft(i) + P[k].r - P[i].l, // findRight(i) + P[i].r - P[k].r); } if (-1 != down) { if (P[k].h - P[down].h > MAX) return INF; if (leftMinTime[down] == -1) { leftMinTime[down] = findLeft(down); } if (rightMinTime[down] == -1) { rightMinTime[down] = findRight(down); } return P[k].h - P[down ].h + min( leftMinTime[down] + P[k].r - P[down].l, rightMinTime[down] + P[down].r - P[k].r); } if (P[k].h > MAX) return INF; else return P[k].h; } int findLeft(int k) { int down = -1; forn(i, k + 1, N + 1) if ((P[k].l - P[i].r) * (P[k].l - P[i].l) <= 0) { down = i; break; // if( P[k].h - P[i].h > MAX) // return INF; // return P[k].h - P[i].h + min( findLeft(i) + P[k].r - P[i].l, // findRight(i) + P[i].r - P[k].r); } if (-1 != down) { if (P[k].h - P[down].h > MAX) return INF; if (leftMinTime[down] == -1) { leftMinTime[down] = findLeft(down); } if (rightMinTime[down] == -1) { rightMinTime[down] = findRight(down); } return P[k].h - P[down].h + min( leftMinTime[down] + P[k].l - P[down].l, rightMinTime[down] + P[down].r - P[k].l); } if (P[k].h > MAX) return INF; else return P[k].h; } |
