POJ1961 | 哈喽哈咯

Written by razrlele 13:41 October 7, 2015

POJ1961

Period

Time Limit: 3000MS		Memory Limit: 30000K
Total Submissions: 15006		Accepted: 7158

Description

For each prefix of a given string S with N characters (each character has an ASCII code between 97 and 126, inclusive), we want to know whether the prefix is a periodic string. That is, for each i (2 <= i <= N) we want to know the largest K > 1 (if there is one) such that the prefix of S with length i can be written as A^K ,that is A concatenated K times, for some string A. Of course, we also want to know the period K.

Input

The input consists of several test cases. Each test case consists of two lines. The first one contains N (2 <= N <= 1 000 000) – the size of the string S.The second line contains the string S. The input file ends with a line, having the
number zero on it.

Output

For each test case, output “Test case #” and the consecutive test case number on a single line; then, for each prefix with length i that has a period K > 1, output the prefix size i and the period K separated by a single space; the prefix sizes must be in increasing order. Print a blank line after each test case.

Sample Input

aaa

aabaabaabaab

Sample Output

Test case #1

2 2

3 3

Test case #2

2 2

6 2

9 3

12 4

Source

Southeastern Europe 2004

题意

给一个字符串，然后问字符串的不同长度前缀子串最多能有多少个循环体（只有在有大于1个的循环体的时候才输出），比如给出的字符串是 aabaabaabaab，从前缀长度为2的字符串即aa开始，最短的循环体是a，循环次数为两次，那么就输出2 2，前缀长度为3的时候则没有循环体不输出，然后前缀长度为6的时候即aabaab，最短的循环体是aab，循环次数是2，同理前缀长度分别9 和 12的时候输出3 和 4 。

思路

运用KMP算法中的next数组，假设前缀长度长度为i，那么只有在 i % (i – next[i] ) == 0 && i / (i – next[i]) > 1的时候才输出答案。

关于KMP算法，可以参考Matrix67的博客，比数据结构课本上讲的确实清楚多了。

这个题用KMP算法确实有点巧，首先KMP算法中的next[i] 表示字符串中的 S[1…next[i]] == S[i-next[i] …i]

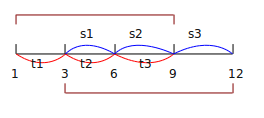
当 i % (i – next[i]) == 0 时，考虑 i == 12，next[i] == 9：

(图片来自 AC_Von的博客 )

则 t1+t2+t3 == s1+s2+s3

又因为 s1 == t2 && s2 == t3

所以 s3 == t1

字符串四部分均相等

代码

* File Name: poj1961.cpp

* Author: razrLeLe

* Mail: razrlele@gmail.com

#include <vector>

#include <set>

#include <deque>

#include <queue>

#include <algorithm>

#include <functional>

#include <iostream>

#include <cstdio>

#include <cmath>

#include <cstdlib>

#include <string>

#include <cstring>

#include <string.h>

#include <map>

#include <cctype>

#include <list>

#include <stack>

#define forn(i, m, n) for( int i = int(m); i < int(n); i++ )

typedef long long ll;

using namespace std;

#define INF 0x3f3f3f3f

#define LOCAL

const int maxn = 1000007;

char in_str[maxn];

int next[maxn];

int len;

void findNext(){

int j = 0;

int k = -1;

next[0] = -1;

while( j < len ){

if( k == -1 || in_str[j] == in_str[k] ){

j++; k++; next[j] = k;

}

else {

k = next[k];

}

return ;

}

int main(int argc, char ** argv)

{

#ifdef LOCAL

freopen("/home/razrlele/build/data.txt", "r", stdin);

freopen("/home/razrlele/build/out.txt", "w", stdout);

#endif

int count = 0;

while( scanf("%d", &len) && len ){

scanf("%s", in_str);

findNext();

if( count ){

printf("\n");

}

printf("Test case #%d\n", ++count);

for( int i = 2; i <= len; i++){

int t = i % (i-next[i]);

int k = i / (i-next[i]);

if( t == 0 && k > 1 )

printf("%d %d\n", i, k);

}

return 0;

}

参考

AC_Von的博客