UVAOJ699

UVAOJ699

699 – The Falling Leaves Time limit: 3.000 seconds

The Falling Leaves

Each year, fall in the North Central region is accompanied by the brilliant colors of the leaves on the trees, followed quickly by the falling leaves accumulating under the trees. If the same thing happened to binary trees, how large would the piles of leaves become?
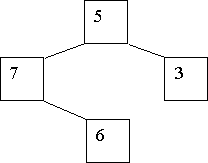
We assume each node in a binary tree “drops” a number of leaves equal to the integer value stored in that node. We also assume that these leaves drop vertically to the ground (thankfully, there’s no wind to blow them around). Finally, we assume that the nodes are positioned horizontally in such a manner that the left and right children of a node are exactly one unit to the left and one unit to the right, respectively, of their parent. Consider the following tree:

The nodes containing 5 and 6 have the same horizontal position (with different vertical positions, of course). The node containing 7 is one unit to the left of those containing 5 and 6, and the node containing 3 is one unit to their right. When the “leaves” drop from these nodes, three piles are created: the leftmost one contains 7 leaves (from the leftmost node), the next contains 11 (from the nodes containing 5 and 6), and the rightmost pile contains 3. (While it is true that only leaf nodes in a tree would logically have leaves, we ignore that in this problem.)

Input 

The input contains multiple test cases, each describing a single tree. A tree is specified by giving the value in the root node, followed by the description of the left subtree, and then the description of the right subtree. If a subtree is empty, the value -1 is supplied. Thus the tree shown above is specified as 5 7 -1 6 -1 -1 3 -1 -1. Each actual tree node contains a positive, non-zero value. The last test case is followed by a single -1 (which would otherwise represent an empty tree).

Output 

For each test case, display the case number (they are numbered sequentially, starting with 1) on a line by itself. On the next line display the number of “leaves” in each pile, from left to right, with a single space separating each value. This display must start in column 1, and will not exceed the width of an 80-character line. Follow the output for each case by a blank line. This format is illustrated in the examples below.

Sample Input 

Sample Output 

---

Miguel Revilla
2000-08-14

题目的意思是把在同一垂直线上的树的结点定义为一个落叶堆，要求求出各个堆上的结点值之和。

直接给每个节点加一个水平坐标值就可以了

比如题目中的那颗树中：

5（根节点）的水平坐标值设为0，7设为-1，3设为1,那么6的水平坐标就是0，以此类推，然后再用map搞一搞就O了。