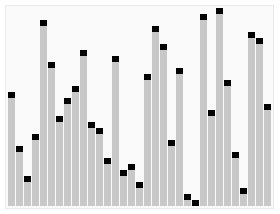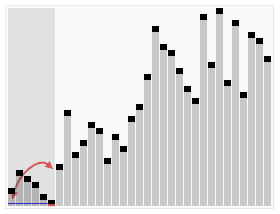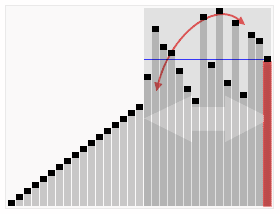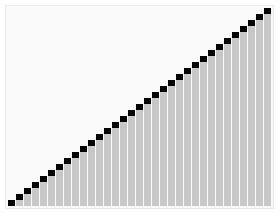
Simple implementation of five common sorting algorithm in Python.
Bubble Sort
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- class Solution(object): def bubble_sort(self, array): for i in range(len(array)): for j in range(i+1, len(array)): if array[j] < array[i]: array[i], array[j] = array[j], array[i] return array print(Solution().bubble_sort([2,8,7,1,3,5,6,4])) |
Best/Worst/Average Time Complexity:\(O(n^{2})/O(n^{2})/O(n^{2})\)
Memory Complexity: \(O(n)\)
Selection Sort
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- class Solution(object): def selection_sort(self, array): for i in range(0, len(array)-1): for j in range(i+1, len(array)): if array[i] > array[j]: array[i], array[j] = array[j], array[i] return array print(Solution().selection_sort([2,8,7,1,3,5,6,4])) |
Best/Worst/Average Time Complexity: \(O(n^{2})/O(n^{2})/O(n^{2})\)
Memory Complexity: \(O(n)\)
Insertion Sort
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- class Solution(object): def insertion_sort(self, array): for i in range(1, len(array)): key = array[i] j = i-1 while j >= 0 and array[j] > key: array[j+1] = array[j] j -= 1 array[j+1] = key return array print(Solution().insertion_sort([2,8,7,1,3,5,6,4])) |
Best/Worst/Average Time Complexity: \(O(n)/O(n^{2})/O(n^{2})\)
Memory Complexity: \(O(n)\)
Quick Sort
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- class Solution(object): def partition(self, array, p, r): x = array[r] i = p - 1 for j in range(p, r): if array[j] <= x: i += 1 array[i], array[j] = array[j], array[i] array[i+1], array[r] = array[r], array[i+1] return i+1 def quick_sort(self, array, p, r): if p < r: q = self.partition(array, p, r) self.quick_sort(array, p, q-1) self.quick_sort(array, q+1, r) return array print(Solution().quick_sort([2,8,7,1,3,5,6,4], 0, 7)) |
Best/Worst/Average Time Complexity: \(O(n\log {(n)})/O(n^{2})/O(n\log {(n)})\)
Worst/Average Memory Complexity: Not Sure
Heap Sort
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- class Solution(object): def heap_sort(self, array, count): self.heapify(array, count) end = count-1 while end > 0: array[end], arrays[0] = array[0], array[end] end = end-1 self.siftDown(array, 0, end) return array def heapify(self,array, count): start = count-1 while start >= 0: self.siftDown(array, start, count-1) start -= 1 def siftDown(self, array, start, end): root = start iLeftChild = lambda x:x*2+1 iRightChild = lambda x:x*2+2 while iLeftChild(root) <= end : child = iLeftChild(root) swap = root if array[root] < array[child]: swap = child if child+1 <= end and array[swap] < array[child+1]: swap = child+1 if swap == root : return else: array[root], array[swap] = array[swap], array[root] root = swap print(Solution().heap_sort([2,8,7,1,3,5,6,4], 8)) |
Best/Worst/Average Time Complexity: \(O(n\log {(n)})/O(n\log {(n)})/O(n\log {(n)})\)
Memory Complexity: \(O(n)\)
References
https://en.wikipedia.org/wiki/Bubble_sort
https://en.wikipedia.org/wiki/Selection_sort
https://en.wikipedia.org/wiki/Insertion_sort